java复习与提升(11)-----递归的简单例子

简单一句话

java 递归

个人是很怕递归的，现在专门拿出一个博文来说这个东西，本人脑子不是很灵活，喜欢把所有的问题刻板化，下面我就尝试把递归也给刻板化
目前个人的理解是，如果有一些问题需要用递归来解决，那么首先我们应该找到它的递推项，有了递推项就比较好写代码
下面一边练习例子，一边来总结递归的想法
例子一

请用递归的方法，从1打印到10，然后从10打印到1
这个用for循环很容易就实现了，我们看一下用递归怎么实现
package Recursive;

public class PrintNum {
    // printInOrder(10) 是打印1 2 3 4 5 6 7 8 9 10
    // printInOrder(9)  是打印1 2 3 4 5 6 7 8 9
    // 也就是说 printInOrder(10) = printInOrder(9) + print(10)
    public void printInOrder(int num){
        if(num > 1){
            printInOrder(num-1);
        }
        System.out.println(num);
    }
    public static void main(String[] args) {
        PrintNum print = new PrintNum();
        print.printInOrder(10);
    }
}思路已经附在代码中了，我们找递推项，我们的函数printInOrder(10)是将数从1打印到10
那么如果我们想做成这个事情，就要先从1打印到9，也就是先要完成printInOrder(9)
因此我们的递推式应该是这样：printInOrder(10) = printInOrder(9) + print(10)
任何一个递推式都应该有返回，那么我们什么时候返回呢？也就是当num为1的时候，就应该执行print(1)来打印了，因此当num为1的时候就应该终止递归
顺着这个思路我们有了上面的代码，运行输出后为：
1
2
3
4
5
6
7
8
9
10从1打印到10我们完成了，再来看从10打印到1
package Recursive;

public class PrintNum {
    // printInOrder(10) 是打印1 2 3 4 5 6 7 8 9 10
    // printInOrder(9)  是打印1 2 3 4 5 6 7 8 9
    // 也就是说 printInOrder(10) = printInOrder(9) + print(10)
    public void printInOrder(int num){
        if(num > 1){
            printInOrder(num-1);
        }
        System.out.println(num);
    }
    // printReverseOrder(10) 是打印10 9 8 7 6 5 4 3 2 1
    // printReverseOrder(9)  是打印 9 8 7 6 5 4 3 2 1
    // 也就是说 printReverseOrder(10) = print(10) + printReverseOrder(9)
    public void printReverseOrder(int num){
        System.out.println(num);
        if(num > 1){
            printReverseOrder(num-1);
        }
    }
    public static void main(String[] args) {
        PrintNum print = new PrintNum();
        print.printInOrder(10);
        System.out.println("======================================");
        print.printReverseOrder(10);
    }
}思路附在代码注释中了，和上面的顺序打印的思路大差不差，就不再赘述
这样输出的是
1
2
3
4
5
6
7
8
9
10
======================================
10
9
8
7
6
5
4
3
2
1总结例子一，我们可以知道用递归解决问题的思维步骤：
①分析问题
②找到递推项
③思考结束递归的条件
④写代码
例子二

阶乘，比如，5! = 5*4*3*2*1
代码如下：
package Recursive;

public class Factorial {
    // !(10) = 10 * !(9)
    // 当 num == 1 的时候, !(1) = 1
    public int getFactorial(int num){
        if (num == 1){
            return 1;
        } else {
            return num*getFactorial(num-1);
        }
    }

    public static void main(String[] args) {
        Factorial tool = new Factorial();
        System.out.println("The output of !(5) is :  " + tool.getFactorial(5));
        System.out.println("The output of !(10) is :  " + tool.getFactorial(10));
    }
}看一下思考问题的步骤：
① 分析问题，阶乘，就是从1乘到目标数
② 递推项，也就是说，getFactorial(10) = 10*getFactorial(9)，也就是说getFactorial(n) = n*getFactorial(n-1)
③ 思考问题结束的条件，getFactorial(1) = 1
④ 写出上面的代码，并进行调试
输出的结果是：
The output of !(5) is :  120
The output of !(10) is :  3628800例子三

请使用递归的方式打印出规定个数的斐波那契数
看一下思考问题的步骤：
① 分析问题，斐波那契数列，有递归关系的不是数列，而是里面的元素
② 递推项，也就是说，getFibonacci(num) = getFibonacci(num-1) + getFibonacci(num-2)
③ 思考问题结束的条件，getFactorial(1) = getFactorial(2) = 1
④ 写出下面的代码并调试
package Recursive;

public class Fibonacci {

    // 如果是直接得到一个Fibonacci数列不是很好获得
    // 因为我们找不到很明显的递推项, 假如 getFibonacci(num) 这个方法是得到num个Fibnacci数组成的数列
    // getFibonacci(num)无法由getFibonacci(num-1)或者getFibonacci(num-2)或者之前的数列来直接得到
    // 但是Fibonacci中的数我们是可以较为轻易得到的
    // 假如getFibonacci(num)方法产生的数代表第num个Fibonacci中的数
    // 可以得到递推项 getFibonacci(num) = getFibonacci(num-1) + getFibonacci(num-2)
    // 但是Fibonacci中的第一个数和第二个数不在这个递推项范围内, 也就是说 getFibonacci(1) = 1, getFibonacci(2) = 1
    public int getFibonacci(int num){
        if(num <= 2){
            return 1;
        } else {
            return getFibonacci(num-1)+getFibonacci(num-2);
        }
    }

    public void printFibonacci(int num){
        for(int i=0; i<num; i++){
            System.out.print(getFibonacci(i+1));
            System.out.print("  ");
        }
    }

    public static void main(String[] args) {
        Fibonacci Fib = new Fibonacci();
        Fib.printFibonacci(10);
    }
}输出的是：
1  1  2  3  5  8  13  21  34  55例子四

猴子吃桃问题：有一堆桃子，猴子第一天吃了其中的一半，并在多吃了一个， 以后每天猴子都吃其中的一半，然后再多吃一个。当到第10天时，想再吃时(即还没吃)，发现只有1个桃子了，问题：最初共有多少个桃子？
package Recursive;

public class MonkeyEatPeach {
    // 问题让我们求出最开始的桃子数量
    // 我们可以反过来想, 也就是猴子吐桃子
    // 每天猴子从肚子中先吐一个桃子, 然后再基于已有的数量吐出另外一半
    // peachAll方法统计第m天有多少个桃子, 于是我们可以写出递推式
    // peachAll(m) = 2*(peachAll(m-1) + 1)
    // 这个递归函数的退出条件就是 peachAll(1) = 1 , 第一天就只有1个桃子
    public int peachAll(int day){
        if(day == 1){
            return 1;
        } else {
            return 2*(peachAll(day-1) + 1);
        }
    }

    public static void main(String[] args) {
        MonkeyEatPeach monkey = new MonkeyEatPeach();
        System.out.println("The number of peach is : " + monkey.peachAll(10));
    }
}看一下思考问题的步骤：
① 分析问题，猴子吃桃子，最后还有1个没吃，求最开始的桃子数量，每次吃一半多一个
② 根据这个每次吃一半多一个我们就足够写出递推项 peachAll(m) = 2*(peachAll(m-1) + 1)
③ 思考问题结束的条件，peachAll(1) = 1
④ 写出上面的代码并调试
输出的是：
The number of peach is : 1534例子五

老鼠出迷宫问题，有一个老鼠从蓝色的点开始移动，它要到达绿色的点处，能否找到一条路径
注意不能斜着走，只能以上下左右的方式走



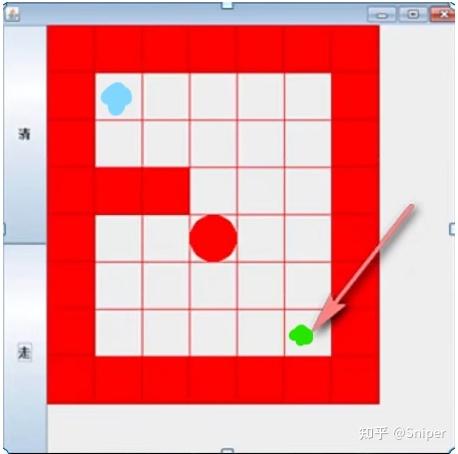
韩顺平java课程截图

很有意思的题目，用递归来解决，看代码：
package Recursive;

public class Maze {

    // 初始化迷宫二维数组
    public int[][] initializeMaze(int row, int col){
        int[][] mazeForMouse = new int[row][col];
        // 描绘障碍物
        for(int i=0; i<col; i++){
            mazeForMouse[0] = 1;
            mazeForMouse[row-1] = 1;
        }
        for(int i=0; i<row; i++){
            mazeForMouse[0] = 1;
            mazeForMouse[col-1] = 1;
        }
        mazeForMouse[3][1] = 1;
        mazeForMouse[3][2] = 1;
        mazeForMouse[4][3] = 1;
        // 将整个二维数组打印
        for(int i=0; i<row; i++){
            for(int j=0; j<col; j++){
                System.out.print(mazeForMouse[j]);
            }
            System.out.println();
        }
        return mazeForMouse;
    }

    // 迷宫问题就感觉我们在拿着手电筒进行探测
    // 我们不知道前面的路通向哪里, 能不能走通, 但是我们知道的是已经走过的路能不能走通
    // 就这样一点一点探寻出口, 边走边做标记
    // 迷宫中的0代表没有障碍物, 1代表有障碍物去不了
    // 我们用2代表自己走过的且能走通的路, 用3标记那些走死的路
    // 现在迷宫问题被我们改变成了标记问题
    // 思考递推项: 我们令findRoute函数为标记地图上所有的地块  
    //            findRoute(all) = findRoute(第一块) + findRoute(周围的块)
    //            我们所要做的是标记地块是2还是3, 如果在地块的四周都找不到路则本地块标为3
    //            怎样通知上面的函数找不到路呢? 因此返回值应当是boolean, 告诉调用它的函数找不找的到路
    // 思考递归的结束: 当将出口标记为2的时候, 就说明我们找到路了
    public boolean findRoute(int rowNum, int colNum, int[][] maze){
        //确定递归结束的条件, 当maze[6][5]为2就不找了, 因此要用if else来限定
        if (maze[6][5] == 2) {
            return true;
        } else {
            // 现在开始标记地块, 先确定当前的地块上没有障碍物, 而且是没有走过的, 而且不是死路
            if (maze[rowNum][colNum] == 0) {
                // 先假定当前的地块是可以走的
                maze[rowNum][colNum] = 2;
                if (findRoute(rowNum+1, colNum, maze)) {  // 按照下、右、上、左的顺序来找
                    return true;
                } else if (findRoute(rowNum, colNum+1, maze)) {
                    return true;
                } else if (findRoute(rowNum-1, colNum, maze)) {
                    return true;
                } else if (findRoute(rowNum, colNum-1, maze)) {
                    return true;
                } else {
                    maze[rowNum][colNum] = 3;
                    return false;
                }
            } else { //这说明标记是1, 2, 3  ( 1是障碍物当返回false, 2是走过的路就返回false别再判断了, 3是走不同的路当返回false )
                return false;
            }
        }
    }

    public static void main(String[] args) {
        Maze mouseMaze = new Maze();
        int[][] completedMaze = mouseMaze.initializeMaze(8, 7);
        mouseMaze.findRoute(1, 1, completedMaze);
        System.out.println("===========================================");
        // 将整个二维数组打印
        for(int i=0; i<8; i++){
            for(int j=0; j<7; j++){
                System.out.print(completedMaze[j]);
            }
            System.out.println();
        }
    }
}输出的是：
1111111
1000001
1000001
1110001
1001001
1000001
1000001
1111111
===========================================
1111111
1200001
1222001
1112201
1001201
1000201
1000221
1111111看一下思考问题的步骤：
①分析问题：
有的时候，用递归并不能直接解决问题，比如我们在斐波那契数列中就发现了这个问题
我们需要将解决其它递归问题从而转化成此类问题
迷宫问题就感觉我们在拿着手电筒进行探测，我们不知道前面的路通向哪里, 能不能走通, 但是我们知道的是已经走过的路能不能走通，就这样一点一点探寻出口, 边走边做标记。
规定迷宫中的0代表没有障碍物, 1代表有障碍物去不了，我们用2代表自己走过的且能走通的路, 用3标记那些走死的路 现在迷宫问题被我们改变成了标记问题
而这个标记问题，我们可以直接用递归来解决
②思考递推项：
我们令findRoute函数为标记地图上所有的地块
findRoute(all) = findRoute(第一块) + findRoute(周围的块)
第一块是否能走，取决于第一块是否是障碍物，或者它周围的块能不能走，如果第一块不是障碍物，并且周围的块能走，那么第一块就能走
怎样通知找第一块的函数，它周围的块找不找的到路呢? 因此返回值应当是boolean, 告诉调用它的函数找不找的到路
③思考结束递归条件
当将出口标记为2的时候, 就说明我们找到路了
④写出上面的代码并调试
例子六

永远的汉诺塔问题：



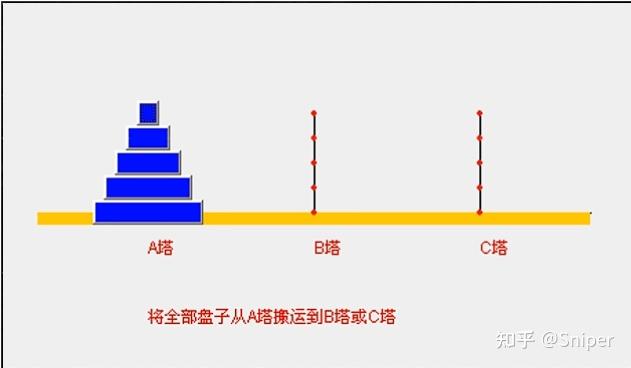
韩顺平java课程截图

问题很简单，将A塔中的5个盘子移动到C塔上，但是注意，一次只能移动一个盘子，另外，小盘子必须放在大盘子上面，要不然小盘子就会碎
这个问题多次伤害了我，学一次忘一次，这次记录下来，来看代码：
package Recursive;

public class HanoiTower {

    // 我们假设函数move, 是将盘子从a塔移动到c塔, 假设a塔中的盘子数量为m
    // 这样的话move(m, a, b, c), 就是从a塔开始, 借助b塔, 然后移动到c塔
    // 因为大盘子必须在下面的缘故, 我们必须先将大盘子移动到c塔, 不然盘子会碎
    // 因此问题就转化为了将move(m-1, a, c, b) 也就是将m-1个盘子从a塔借助c塔送到b塔
    // 然后将 A -> C
    // 最后再将move(m-1, b, a, c) 也就是将m-1个盘子从b塔借助a塔送到c塔
    // 我们思考递推项: move(m, a, b, c) = move(m-1, a, c, b) + move(1, a, c) + move(m-1, b, a, c)
    // 递归结束的最终条件就是 当哪个盘子掉到1个的时候, 将它移到c盘子
    public void move(int num, char a, char b, char c) {
        if (num == 1) {
            System.out.println(a+" --> "+c);
        } else {
            move(num-1, a, c, b);
            System.out.println(a+" --> "+c);
            move(num-1, b, a, c);
        }
    }

    public static void main(String[] args) {
        HanoiTower tower = new HanoiTower();
        tower.move(5, 'A', 'B', 'C');
    }
}看一下思考问题的步骤：
①分析问题：由于大盘子必须在小盘子下面，因此想要将5个盘子移动到c塔，必须首先将最大的盘子移动到c塔。这样的话其余的四个盘子必须先移动到b塔，也就是将5个盘子从a塔移到c塔的问题，变成了将4个盘子从a塔移动到b塔
②思考递推项：在分析问题中其实已经揭示了规则。很容易将递推项写出来，
move(num, a, b, c)意思是，将 num 个盘子从a塔开始，借助b塔，移动到c塔
move(num, a, b, c) = move(num-1, a, c, b) + move(1, a, c) + move(num-1, b, a, c)
③思考结束项，当num==1时，直接从a移动到c就好
④写出上面的代码并调试
输出的结果是：
A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C例子七

八皇后问题：在8×8格的国际象棋上摆放八个皇后，使其不能相互攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法



韩顺平java课程

看一下思考问题的步骤：
①分析问题：理论上要用二维数组来表示棋盘，但是我们可以进行简化。就用一维数组表示即可。因为这八个皇后只可能在八个不同的行。因此用colArr[row]，row的取值范围是0-7，这样就是可以表示这八个棋子的位置。
这个问题其实很像例子五，个人感觉都属于探测问题。就是先找一个，然后判断这一个能不能达标，因此我们可以写出递推式
②递推式：layTheQueen(8) = layTheQueen(1) + layTheQueen(remain)
同时，因为要告知上一个函数能否放置，因此返回值必须是boolean
③思考结束递归时的情况：当放完了八个棋子时，递归结束，进行打印
④写出如下代码并进行调试
package Recursive;

public class EightQueen {

    public int[] initial(){
        int[] colArr = new int[8];
        return colArr;
    }

    public boolean judge(int row, int[] colArr, int decide){
        for(int i=0; i<row; i++){
            if(colArr == decide || Math.abs(i-row) == Math.abs(colArr-decide)){
                return false;
            }
        }
        return true;
    }

    public boolean layTheQueen(int row, int[] colArr){
        if (row > 7){
            // 打印结果数组
            for(int j=0; j<row; j++){
                System.out.print(colArr[j]+"  ");
            }
            System.out.println();
            return false;
        } else {
            for(int i=0; i<8; i++){
                if (judge(row, colArr, i)){
                    colArr[row] = i;
                    if(layTheQueen(row+1, colArr)){      
                        return true;
                    }
                }
            }
            return false;
        }
    }


    public static void main(String[] args) {
        EightQueen queen = new EightQueen();
        int[] array = queen.initial();
        queen.layTheQueen(0, array);

    }
}输出的是:
0  4  7  5  2  6  1  3  
0  5  7  2  6  3  1  4  
0  6  3  5  7  1  4  2  
0  6  4  7  1  3  5  2  
1  3  5  7  2  0  6  4  
1  4  6  0  2  7  5  3  
1  4  6  3  0  7  5  2  
1  5  0  6  3  7  2  4  
1  5  7  2  0  3  6  4
1  6  2  5  7  4  0  3  
1  6  4  7  0  3  5  2
1  7  5  0  2  4  6  3
2  0  6  4  7  1  3  5
2  4  1  7  0  6  3  5
2  4  1  7  5  3  6  0
2  4  6  0  3  1  7  5
2  4  7  3  0  6  1  5
2  5  1  4  7  0  6  3
2  5  1  6  0  3  7  4
2  5  1  6  4  0  7  3
2  5  3  0  7  4  6  1  
2  5  3  1  7  4  6  0
2  5  7  0  3  6  4  1
2  5  7  0  4  6  1  3
2  5  7  1  3  0  6  4
2  6  1  7  4  0  3  5
2  6  1  7  5  3  0  4
2  7  3  6  0  5  1  4
3  0  4  7  1  6  2  5
3  0  4  7  5  2  6  1  
3  1  4  7  5  0  2  6
3  1  6  2  5  7  0  4
3  1  6  2  5  7  4  0
3  1  6  4  0  7  5  2
3  1  7  4  6  0  2  5
3  1  7  5  0  2  4  6
3  5  0  4  1  7  2  6
3  5  7  1  6  0  2  4
3  5  7  2  0  6  4  1
3  6  0  7  4  1  5  2
3  6  2  7  1  4  0  5
3  6  4  1  5  0  2  7
3  6  4  2  0  5  7  1
3  7  0  2  5  1  6  4
3  7  0  4  6  1  5  2
3  7  4  2  0  6  1  5
4  0  3  5  7  1  6  2  
4  0  7  3  1  6  2  5
4  0  7  5  2  6  1  3
4  1  3  5  7  2  0  6
4  1  3  6  2  7  5  0
4  1  5  0  6  3  7  2
4  1  7  0  3  6  2  5
4  2  0  5  7  1  3  6
4  2  0  6  1  7  5  3
4  2  7  3  6  0  5  1
4  6  0  2  7  5  3  1
4  6  0  3  1  7  5  2
4  6  1  3  7  0  2  5
4  6  1  5  2  0  3  7
4  6  1  5  2  0  7  3
4  6  3  0  2  7  5  1  
4  7  3  0  2  5  1  6
4  7  3  0  6  1  5  2
5  0  4  1  7  2  6  3
5  1  6  0  2  4  7  3
5  1  6  0  3  7  4  2
5  2  0  6  4  7  1  3
5  2  0  7  3  1  6  4
5  2  0  7  4  1  3  6
5  2  4  6  0  3  1  7
5  2  4  7  0  3  1  6
5  2  6  1  3  7  0  4
5  2  6  1  7  4  0  3
5  2  6  3  0  7  1  4
5  3  0  4  7  1  6  2
5  3  1  7  4  6  0  2
5  3  6  0  2  4  1  7
5  3  6  0  7  1  4  2  
5  7  1  3  0  6  4  2
6  0  2  7  5  3  1  4
6  1  3  0  7  4  2  5
6  1  5  2  0  3  7  4
6  2  0  5  7  4  1  3
6  2  7  1  4  0  5  3
6  3  1  4  7  0  2  5
6  3  1  7  5  0  2  4
6  4  2  0  5  7  1  3
7  1  3  0  6  4  2  5
7  1  4  2  0  6  3  5
7  2  0  5  1  4  6  3
7  3  0  2  5  1  6  4这时七个很简单也是很基础的例子，虽然我绞尽了脑汁才解决了这几个问题，继续加油吧！